Modeling and Control of Piezoelectric Flextensional Actuators
Executive Summary
Many applications mandate precise position control on the order of micrometer to nanometer resolution. Atomic force microscopy, micro-machining/precision grinding, and adaptive optics are a few such applications. Piezoelectric-based actuators typically possess the bandwidth and displacement resolution needed for such applications. However, they can rarely meet performance objectives without closed-loop control algorithms, and dynamic models of systems are the basis around which control algorithms are formed.
Piezoelectric flextensional actuators offer increased displacement over typical piezostack actuators, and increased block force over bimorph piezo actuators. By developing a dynamic model of a commercially available flextensional actuator, a control scheme can be designed to command its displacement trajectory. This will enable the actuator to meet the needs of the previously mentioned applications.
Primary Project Objectives
1) Experimentally characterize piezoelectric flextensional actuator.
2) Create a dynamic model of the actuator that captures the modes, zeros, low frequency behavior, etc. revealed in the experimental data.
3) Using the model, design a closed-loop controller that will command the position of the actuator’s working surface.
4) Test controller in real time and compare actual results to simulated results.
Research Description
The flextensional actuator is comprised of a piezostack actuator integrated into a metal shell. Applying a positive voltage causes an extension of the piezostack. This flexes the metal shell, forcing the working surface downward, yielding a change in position. Applying a negative voltage has exactly the opposite effect. This is shown schematically in the figure below.
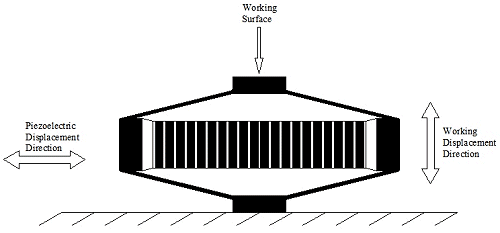
By applying a swept sinusoid, or a chirp signal, the device can be characterized, revealing modes and zeros as well as high and low frequency behavior. Using the input/output data from this type of experiment, a model can be derived that simulates the dynamic output of the actuator based on a user defined input. System identification is the process by which this model is created. A model structure is selected. Model order is then systematically determined. The model parameters are estimated by either a least squares or a numerical optimization algorithm. In the case of the numerical optimization, the objective is to accurately recreate another experimental data set.
A closed-loop control system that commands the working surface position trajectory can be designed around this model. This will allow the actuator to operate with the precision needed for applications such as micro-machining or atomic force microscopy. After a controller is designed it can be applied to the real actuator. Actual closed-loop performance can be assessed and compared the simulated closed-loop system.
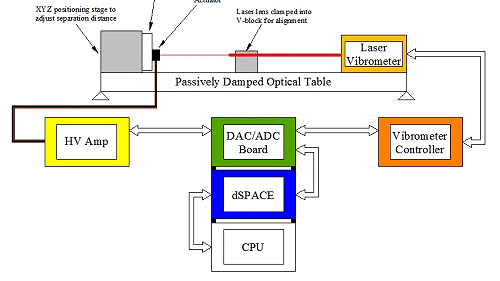
Due to the scale of the measurements (on the order of micrometers or less), the experiment must be isolated. The actuator and the sensor used to track its displacement reside on a passively damped optical table to isolate movements and measurements from background vibrations. The experimental schematic and actual geometric layout of components on the table are shown in the figure below and photograph left.
